home |
the links mine |
6502 primer
intro: integer math & tables |
math table files' descriptions |
rational-number approximations |
how Intel Hex files work |
how the files were calc'd & formed
Large Look-up Tables for Fast, Accurate, 16-Bit Fixed-Point/Scaled-Integer Math
This tells about the files of large look-up tables to put in EPROM.
It is impractical to consider doing tables larger than 64K cells (ie, having inputs of more than 16 bits). The next semi-logical
size up would be 24-bit, meaning most individual tables would require 48MB of memory, which is a lot of ROMs even in 2012.
The ROM bank numbers can be changed by hand. The lines that give the bank number say :02000002xxxxcs, where xxxx is the offset
(like to go into bank 1, the offset is $1:0000, so you put 1000, dropping the last 0) and cs is the checksum. If the table has
more than one bank (as most do), remember you'll need to fix the other bank numbers too, to go in order.
Standard lines you can edit-in for changing offsets for a 1Mx8 EPROM are:
:020000020000FC (for bank 0)
:020000021000EC (for bank 1)
:020000022000DC (for bank 2)
:020000023000CC (for bank 3)
:020000024000BC (for bank 4)
:020000025000AC (for bank 5)
:0200000260009C (for bank 6)
:0200000270008C (for bank 7)
:0200000280007C (for bank 8)
:0200000290006C (for bank 9)
:02000002A0005C (for bank A)
:02000002B0004C (for bank B)
:02000002C0003C (for bank C)
:02000002D0002C (for bank D)
:02000002E0001C (for bank E)
:02000002F0000C (for bank F)
There's a summary at the bottom of the page of which tables are in which EPROMs as I supply them. If you do your own, you can
of course edit the offsets per the above lines to put them in any order you like. To find the offset lines in the files, do a
search for ":02000002".
The byte order of two- and four-byte cells is reversed, ie, "little-endian," low byte first, for normal 6502 and 65816
operation, one of the things these processors do to improve performance. If you don't want it reversed, the tables with two
bytes per cell (which is most of them) will let you just invert the lsb of the address to get high byte first. Two-byte cells
always start on even-numbered addresses.
If you find a problem with a file, or would like a new file formed, contact me at the email address at the bottom. Unless it's
super straight-forward, give a good explanation of what you want-- the function, domain, and range, and anything else important.
I'm not exactly weak in math, but neither am I a pure mathematician, so don't automatically assume that I totally understand
what you're talking about. Unless otherwise specified, I will scale the input and output to fill out the 65,536 possibilities,
to get all the resolution possible with 16-bit cells. If you post another way for someone to make new table hex files
themselves, let me know so I can link to it.
The files are listed here in the order I put them in the two 1Mx8 EPROMs to sell. The only exception is that the bit-reversing
tables are at the end. If you want to re-arrange the tables for your own use, the only requirement is that LOG2.HEX
immediately follow ATAN.HEX.
SQUARE.HEX is a 256K table of squares, with offsets for programming into banks 0-3 ($0:0000-$3:FFFF) of ROM 0. Input is 16-bit
and output is 32-bit, both unsigned. Besides the obvious, a table of squares can help speed up multiplication.
Consider:
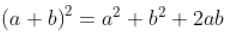 so if you solve for a*b, the multiplication becomes:
so if you solve for a*b, the multiplication becomes:
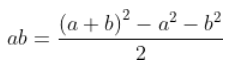 meaning it is reduced to an addition, three squarings (from the table), two subtractions, and a right shift.
There's also the MULT.HEX multiplication table at the end of ROM 1 (at the bottom here).
http://forum.6502.org/viewtopic.php?f=10&t=2211&p=20864#p20864 has an additional note about further simplifying a
multiplication for some situations.
INVERT.HEX is a 256K table of inverses. There are 65,536 cells of 4 bytes each, so input is 16-bit, and output is 32-bit.
Banks 4-7 ($4:0000-7:FFFF) of ROM 0. Looking up the 1st entry (1/0) should not be allowed, but result will show
FFFF:FFFF. Looking up the 2nd entry (1/1) should not be allowed, as the correct answer is 1:0000:0000, which cannot
be shown in 32 bits. Looking up 1/1 will show FFFF:FFFF also. This rounds to the nearest answer. Unsigned.
Inversion eases the otherwise slow division, because to divide, you can multiply by the inverse.
SIN.HEX is the 128K sin table with offsets for programming into banks 8 and 9 ($8:0000-$9:FFFF) of ROM 0. Positive outputs
are limited to $7FFF since $8000 is negative; so there are about 200 $7FFF's (at/near +90°) versus about 112 $8000's
(at/near -90°). The calling routine needs to trap inputs of $3FC7-$4039 unless the error is acceptable. See:
SIN ( $3FC6/2^16 * 360° ) = SIN ( 89.6814° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
SIN ( $3FC7/2^16 * 360° ) = SIN ( 89.6869° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $4039/2^16 * 360° ) = SIN ( 90.3131° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $403A/2^16 * 360° ) = SIN ( 90.3186° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
You can use SIN.HEX for cosines too by just adding $4000 (90°) to the input first.
ASIN.HEX is the 128K arcsin table with offsets for programming into banks A and B ($A:0000-B:FFFF) of ROM 0.
Outputs are limited to ±90° ($C000 to $4000) as on any calculator. Actually, the input range limitation prohibits
reaching +90° output, since +1, represented by $8000, becomes negative. The highest positive input then will be $7FFF,
whose output is $3FAF, or +89.555°. The routine using the table may need to trap that input to prevent an error.
It is important to note that this table is signed in the following way:
0 (represented by a $0000 input) to (nearly) 1 (maximum positive input being represented by $7FFF) outputs 0 (again
represented by $0000) to 89.555° (represented by ($3FAF). The next cell however, which is $8000 cells after the
beginning of the table, is negative, representing -1, and it outputs -90° (represented by $C000). As you advance
through the table from there, you approach 0° from the negative side, so the outputs move toward $FFFF before the
final cell which outputs $0000 as the granularity makes it round to 0°.
If you wanted to change the signing so that it starts at -1 and goes through 0 and goes to +1 without the discontinuity
in the middle, ie, that the table base would be the middle of the table and you go plus or minus from there, you could
edit-in the type-02 Intel Hex offset lines at the beginning of each of the two 64KB sections.
COS.HEX does not exist here. To get the cosine, just add 90° and take the sine.
ACOS.HEX does not exist here either. To get the arccosine, just take the arcsine and subtract the result from 90°.
TAN.HEX does not exist, because of tangent's nasty habit of going to infinity near 90°. To get practical resolution around 0°,
the scale factor would have to be such that the numbers get out of range long before 90°. So to get a tangent, take the
sine and the cosine of the angle, and then the program that needs the tangent can use the fraction as in Forth's */ ,
crank in a scale factor before dividing sine by cosine to get the tangent, or convert to a 32-bit tangent.
ATAN.HEX is the 64K-plus-one-cell table of arctangents for 0-45°, with offsets for programming into bank C ($C:0000-$D:0001)
of ROM 0. Since it takes one additional cell, and the table of base-2 logarithms has no use for a cell 0, that log2
table should follow. Unsigned.
The input is scaled by $8000, so 1.00000 is represented by $8000. 1.00000 is of course the tangent of 45°. The output
is again in the 16-bit circle, but its 45° maximum is represented by $2000. The first 45° are enough to get the rest of
the ±90° like you get with a calculator with a single input, or the whole circle if the calling routine takes in two
signed numbers as a fraction (y/x instead of x,y). (Since the table tops out at 45°, it could be scaled to give 1, 2,
or 3 more bits of precision, but I figured that would unnecessarily complicate things for most operations.)
Because of the problem mentioned above of the tangent easily going out of range near ±90°, it's better to use this
arctangent look-up table for 0-45° and get the rest of the circle from there. Here's how you do that. (I might post
code later.)
For single-number input: If the absolute value of the input is greater than 1.00000 (however you have it scaled),
invert it, look up the arctangent, and subtract that result from 90°. Apply the input sign to the output. As always,
scale factor and range must be heeded.
For dual-number (fractional) input n1/n2: The n1 & n2 are y and x, not vice-versa. Record the signs of the two input
numbers. If both are positive, you're in the 1st (top-right) quadrant (0-90°); if both negative, the 3rd (bottom-left,
180-270°); if n1 (the y value) is the only negative one, then you're in the 4th (bottom-right) quadrant (0 to -90°);
and if n2 (the x value) is the only negative one, then you're in the 2nd (top-left) quadrant (90-180°). Record that,
then take the absolute values of both numbers. If the numerator is greater than the denominator, swap them. Multiply
the numerator (whichever one that is now) by $8000 and divide the double-precision intermediate result by the
denominator, and look up the arctangent value from the table. If you had swapped numerator and denominator first,
subtract the result from 90°. Now you need to put it in the correct quadrant. For 1st quadrant (from above), leave it
alone. For 2nd quadrant, subtract the angle from 180°. For 3rd, add 180°. For 4th, subtract the angle from 360°.
LOG2.HEX is the 128K base-2 log table with offsets for programming into banks D and E ($D:0002-$E:FFFF) of ROM 0. Since you
can't take the log of 0, it has no use for address $D:0000; and since the arctangent table needs it, this log2 table
should immediately follow the arctan table. Input unscaled. Output scaled by 4096. Unsigned.
To get better precision in the base-2 log of smaller numbers, remember that scaling is as easy as shifting at the input
and subtracting at the output. The input is unscaled, going from 1 all the way to 65,535 (which also gives an output
of 65,535); but if the maximum input at some part of your program for example is only 200 and you want better resolution
in the low numbers as well as logs of numbers below 1 (ie, the output is negative), you can make (almost) 256 the
maximum input and scale it by 2^8 or 256 (or $100), then subtract 8*4096 (ie, 32768, or $8000) from the output. Then
the scaled input will have a range of .00390625 to 255.996, and the output range will be -8 (yes, now signed) to +7.9999
instead of 0 to 15.9998 (still scaled by 4096). You can go further, but remember to take care of the signs when the
output becomes so negative that it again becomes positive. Another way to get the negative logs is of course to invert
the input and then make the output negative, which may not even take any extra time if for example you got the input
number by diving two other numbers, and you could just swap the numerator and denominator and maybe use a different
scale factor if appropriate. For logs of numbers very close to 1, the LOG2-A.HEX and LOG2-B.HEX tables are better.
In the remote chance that you need bigger numbers, you can do the opposite, and shift the input to the right and add the
number of the shifts to the output (which will require re-scaling to stay within the 16-bit limitation). But read on...
The LOG2A.HEX file below allows (with more overhead) the forming of the log of any positive non-0 number, since the
integer part of the log is handled by the user's calling routine, and the table only does the fractional part.
BITREV.HEX goes here in bank F of ROM 0, but is described at the end, to keep the continuity in the log tables' descriptions.
ALOG2.HEX is the 128K base-2 antilog table with offsets for programming into banks 0 and 1 ($0:0000-1:FFFF) of ROM 1.
Input scaled by 4096. Output unscaled. Unsigned. For better resolution with smaller inputs and outputs, remember you
can do the reverse of what is discussed above in the LOG2 section above. For antilogs of numbers very close to 0, the
ALOG2-A.HEX and ALOG2-B.HEX tables will be better.
LOG2-A.HEX, with offsets for programming into banks 2 and 3 ($2:0000-3:FFFF) of ROM 1, is a 128K table similar to LOG2.HEX, but
this one leaves the integer part of the log to the user, in order to yield more significant figures. The unsigned
input is limited to the range of 0 to .999985 scaled by 65,536. You cannot take the log of 0 of course; but the 0 here
is the next digit after the first "1" digit found by the user's program as it shifts the input number left until that
first "1" bit is shifted out. You count the number of times you have to shift left for that to happen, and subtract
it from your constant that tells what range you're in, to get the integer part of the log answer. The fractional part
comes from the table, and is scaled the same way. Obviously it requires a little more thought to use this one than
ALOG2.HEX, but the reward is more precision. Answers are rounded to the nearest value that can be represented in the
table.
This can be considered the base-2-log version of the ln(1+X) function sometimes offered on calculators for better
resolution on low numbers. LOG2-B.HEX is a 16x zoom-in on the left end of LOG2-A.HEX. At that point, the worst
output error in LOG2-A.HEX is still under 0.02% from rounding and granularity; and below that point you can get more
resolution back by going to the LOG2-B.HEX table.
Remember that to get the log of numbers below 1, you just invert the argument, then negate the answer.
ALOG2-A.HEX, with offsets for programming into banks 4 and 5 ($4:0000-5:FFFF) of ROM 1, is just the reverse of LOG2-A.HEX
above. The input is the fractional part of the number to get the base-2 antilog of, leaving the integer part to the
user to handle separately, in order to yield more significant figures. So for inputs of 1 (scaled) and higher, strip
off the integer part and keep it aside, look up the antilog of the fractional part in the table, then shift it left by
however many bits the previously stripped-off integer part says (possibly requiring re-scaling). The range of the
unsigned input of the table is 0 to .9999847 scaled by 65,536. The unsigned output also has the same range and scale.
This can be considered the base-2-antilog version of the ex-1 function sometimes offered on calculators for better
resolution on low numbers. ALOG2-B.HEX is a 16x zoom-in on the left end of ALOG2-A.HEX. At that point, the worst
output error in ALOG2-A.HEX is still only about 0.03%; and below that point you can get more resolution back by going
to the ALOG2-B.HEX table.
Remember that to get the antilog of negative numbers, you just change the sign of the argument, then invert the answer.
LOG2-B.HEX, with offsets for programming into banks 6 and 7 ($6:0000-7:FFFF) of ROM 1, is a 128K table that is a zoom-in on
the left end of LOG2-A.HEX, expanded by a factor of 16, so the input has four more significant bits. The unsigned
input is limited to the range of 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576), while
the output range is 0 to .0874615 scaled by 2^19 (ie, 524,288), which comes out to $B31F (45,855 in decimal). So to
clarify: there are 65,536 two-byte cells; but keeping a binary scale factor on the output to keep it more compatible
with LOG2-A.HEX (because it is a zoom-in on its left end) means the output does not reach $FFFF.
Note that LOG2-A.HEX and LOG2-B.HEX are actually the base-2 log version of what is sometimes offered on calculators
as the ln(1+X) function for better resolution for logs of numbers very close to 1 (and very close to 0 in the ln(1+X)
function). If you go below approximately .0015 for input on the LOG2_B.HEX table, you will get the best answer by
simply saying that ln(1+X)≈X (similar to how the sine and the tangent of very small angles are basically the same).
It's not that there's anything wrong with the table, but that with the scaled input and output being only a few hundred
or less, the resolution is lost more and more as you go down. Remember however that the ln(1+X)≈X approximation for
low numbers is for the natural log, whereas the table is for the base-2 log; so convert accordingly!
ALOG2-B.HEX, with offsets for programming into banks 8 and 9 ($8:0000-9:FFFF) of ROM 1, is a 128K table that is basically the
reverse of LOG2-B.HEX, but in this case, a 16x zoom-in on the left end of ALOG2-A.HEX; so the range of its unsigned
input is from 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576). The output then ranges
from 0 to .0442731 also scaled by 2^20, which comes out to $B558 (46,424 in decimal). So to clarify: there are 65,536
two-byte cells; but keeping a binary scale factor on the output to keep it more compatible with ALOG2-A.HEX (because it
is a zoom-in on its left end) means that the output does not reach $FFFF.
Note that ALOG2-A.HEX and ALOG2-B.HEX are actually the base-2 antilog version of what is sometimes offered on
calculators as the ex-1 function for better resolution for antilogs of numbers very close to 0. If you go much below
approximately .001 for input on the ALOG2-B.HEX table, you will get the best answer by simply saying that ex-1≈X
(similar to how the sine and the tangent of very small angles are basically the same). It's not that there's anything
wrong with the table, but that with the scaled input and output being only a few hundred or less, the resolution is
lost more and more as you go down. Remember however that the ex-1≈X approximation for low numbers is for the natural
antilog, whereas the table is for the base-2 antilog; so convert accordingly!
For the ln(1+X) and ex-1 functions, use the LOG2-A.HEX, LOG2-B.HEX, ALOG2-A.HEX, and ALOG2-B.HEX tables, and the notes above
that go with them. Hyperbolic and inverse hyperbolic functions, and certain financial calculations, evaluate the expressions
ln(1+x) and ex-1 for arguments near zero and with results also near zero. The log & antilog tables with the -A and -B in
their file names allow greater accuracy in such calculations. There is a discussion of how to get ex-1 on a calculator
that's lacking that function, on the HP museum calculator forum, at http://hpmuseum.org/forum/thread-5508.html .
ln.HEX does not exist here. For ln (natural log): Since you'll normally have a scale factor anyway, just calculate the ln
(natural log) from the base-2 log. The conversion is:
meaning it is reduced to an addition, three squarings (from the table), two subtractions, and a right shift.
There's also the MULT.HEX multiplication table at the end of ROM 1 (at the bottom here).
http://forum.6502.org/viewtopic.php?f=10&t=2211&p=20864#p20864 has an additional note about further simplifying a
multiplication for some situations.
INVERT.HEX is a 256K table of inverses. There are 65,536 cells of 4 bytes each, so input is 16-bit, and output is 32-bit.
Banks 4-7 ($4:0000-7:FFFF) of ROM 0. Looking up the 1st entry (1/0) should not be allowed, but result will show
FFFF:FFFF. Looking up the 2nd entry (1/1) should not be allowed, as the correct answer is 1:0000:0000, which cannot
be shown in 32 bits. Looking up 1/1 will show FFFF:FFFF also. This rounds to the nearest answer. Unsigned.
Inversion eases the otherwise slow division, because to divide, you can multiply by the inverse.
SIN.HEX is the 128K sin table with offsets for programming into banks 8 and 9 ($8:0000-$9:FFFF) of ROM 0. Positive outputs
are limited to $7FFF since $8000 is negative; so there are about 200 $7FFF's (at/near +90°) versus about 112 $8000's
(at/near -90°). The calling routine needs to trap inputs of $3FC7-$4039 unless the error is acceptable. See:
SIN ( $3FC6/2^16 * 360° ) = SIN ( 89.6814° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
SIN ( $3FC7/2^16 * 360° ) = SIN ( 89.6869° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $4039/2^16 * 360° ) = SIN ( 90.3131° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $403A/2^16 * 360° ) = SIN ( 90.3186° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
You can use SIN.HEX for cosines too by just adding $4000 (90°) to the input first.
ASIN.HEX is the 128K arcsin table with offsets for programming into banks A and B ($A:0000-B:FFFF) of ROM 0.
Outputs are limited to ±90° ($C000 to $4000) as on any calculator. Actually, the input range limitation prohibits
reaching +90° output, since +1, represented by $8000, becomes negative. The highest positive input then will be $7FFF,
whose output is $3FAF, or +89.555°. The routine using the table may need to trap that input to prevent an error.
It is important to note that this table is signed in the following way:
0 (represented by a $0000 input) to (nearly) 1 (maximum positive input being represented by $7FFF) outputs 0 (again
represented by $0000) to 89.555° (represented by ($3FAF). The next cell however, which is $8000 cells after the
beginning of the table, is negative, representing -1, and it outputs -90° (represented by $C000). As you advance
through the table from there, you approach 0° from the negative side, so the outputs move toward $FFFF before the
final cell which outputs $0000 as the granularity makes it round to 0°.
If you wanted to change the signing so that it starts at -1 and goes through 0 and goes to +1 without the discontinuity
in the middle, ie, that the table base would be the middle of the table and you go plus or minus from there, you could
edit-in the type-02 Intel Hex offset lines at the beginning of each of the two 64KB sections.
COS.HEX does not exist here. To get the cosine, just add 90° and take the sine.
ACOS.HEX does not exist here either. To get the arccosine, just take the arcsine and subtract the result from 90°.
TAN.HEX does not exist, because of tangent's nasty habit of going to infinity near 90°. To get practical resolution around 0°,
the scale factor would have to be such that the numbers get out of range long before 90°. So to get a tangent, take the
sine and the cosine of the angle, and then the program that needs the tangent can use the fraction as in Forth's */ ,
crank in a scale factor before dividing sine by cosine to get the tangent, or convert to a 32-bit tangent.
ATAN.HEX is the 64K-plus-one-cell table of arctangents for 0-45°, with offsets for programming into bank C ($C:0000-$D:0001)
of ROM 0. Since it takes one additional cell, and the table of base-2 logarithms has no use for a cell 0, that log2
table should follow. Unsigned.
The input is scaled by $8000, so 1.00000 is represented by $8000. 1.00000 is of course the tangent of 45°. The output
is again in the 16-bit circle, but its 45° maximum is represented by $2000. The first 45° are enough to get the rest of
the ±90° like you get with a calculator with a single input, or the whole circle if the calling routine takes in two
signed numbers as a fraction (y/x instead of x,y). (Since the table tops out at 45°, it could be scaled to give 1, 2,
or 3 more bits of precision, but I figured that would unnecessarily complicate things for most operations.)
Because of the problem mentioned above of the tangent easily going out of range near ±90°, it's better to use this
arctangent look-up table for 0-45° and get the rest of the circle from there. Here's how you do that. (I might post
code later.)
For single-number input: If the absolute value of the input is greater than 1.00000 (however you have it scaled),
invert it, look up the arctangent, and subtract that result from 90°. Apply the input sign to the output. As always,
scale factor and range must be heeded.
For dual-number (fractional) input n1/n2: The n1 & n2 are y and x, not vice-versa. Record the signs of the two input
numbers. If both are positive, you're in the 1st (top-right) quadrant (0-90°); if both negative, the 3rd (bottom-left,
180-270°); if n1 (the y value) is the only negative one, then you're in the 4th (bottom-right) quadrant (0 to -90°);
and if n2 (the x value) is the only negative one, then you're in the 2nd (top-left) quadrant (90-180°). Record that,
then take the absolute values of both numbers. If the numerator is greater than the denominator, swap them. Multiply
the numerator (whichever one that is now) by $8000 and divide the double-precision intermediate result by the
denominator, and look up the arctangent value from the table. If you had swapped numerator and denominator first,
subtract the result from 90°. Now you need to put it in the correct quadrant. For 1st quadrant (from above), leave it
alone. For 2nd quadrant, subtract the angle from 180°. For 3rd, add 180°. For 4th, subtract the angle from 360°.
LOG2.HEX is the 128K base-2 log table with offsets for programming into banks D and E ($D:0002-$E:FFFF) of ROM 0. Since you
can't take the log of 0, it has no use for address $D:0000; and since the arctangent table needs it, this log2 table
should immediately follow the arctan table. Input unscaled. Output scaled by 4096. Unsigned.
To get better precision in the base-2 log of smaller numbers, remember that scaling is as easy as shifting at the input
and subtracting at the output. The input is unscaled, going from 1 all the way to 65,535 (which also gives an output
of 65,535); but if the maximum input at some part of your program for example is only 200 and you want better resolution
in the low numbers as well as logs of numbers below 1 (ie, the output is negative), you can make (almost) 256 the
maximum input and scale it by 2^8 or 256 (or $100), then subtract 8*4096 (ie, 32768, or $8000) from the output. Then
the scaled input will have a range of .00390625 to 255.996, and the output range will be -8 (yes, now signed) to +7.9999
instead of 0 to 15.9998 (still scaled by 4096). You can go further, but remember to take care of the signs when the
output becomes so negative that it again becomes positive. Another way to get the negative logs is of course to invert
the input and then make the output negative, which may not even take any extra time if for example you got the input
number by diving two other numbers, and you could just swap the numerator and denominator and maybe use a different
scale factor if appropriate. For logs of numbers very close to 1, the LOG2-A.HEX and LOG2-B.HEX tables are better.
In the remote chance that you need bigger numbers, you can do the opposite, and shift the input to the right and add the
number of the shifts to the output (which will require re-scaling to stay within the 16-bit limitation). But read on...
The LOG2A.HEX file below allows (with more overhead) the forming of the log of any positive non-0 number, since the
integer part of the log is handled by the user's calling routine, and the table only does the fractional part.
BITREV.HEX goes here in bank F of ROM 0, but is described at the end, to keep the continuity in the log tables' descriptions.
ALOG2.HEX is the 128K base-2 antilog table with offsets for programming into banks 0 and 1 ($0:0000-1:FFFF) of ROM 1.
Input scaled by 4096. Output unscaled. Unsigned. For better resolution with smaller inputs and outputs, remember you
can do the reverse of what is discussed above in the LOG2 section above. For antilogs of numbers very close to 0, the
ALOG2-A.HEX and ALOG2-B.HEX tables will be better.
LOG2-A.HEX, with offsets for programming into banks 2 and 3 ($2:0000-3:FFFF) of ROM 1, is a 128K table similar to LOG2.HEX, but
this one leaves the integer part of the log to the user, in order to yield more significant figures. The unsigned
input is limited to the range of 0 to .999985 scaled by 65,536. You cannot take the log of 0 of course; but the 0 here
is the next digit after the first "1" digit found by the user's program as it shifts the input number left until that
first "1" bit is shifted out. You count the number of times you have to shift left for that to happen, and subtract
it from your constant that tells what range you're in, to get the integer part of the log answer. The fractional part
comes from the table, and is scaled the same way. Obviously it requires a little more thought to use this one than
ALOG2.HEX, but the reward is more precision. Answers are rounded to the nearest value that can be represented in the
table.
This can be considered the base-2-log version of the ln(1+X) function sometimes offered on calculators for better
resolution on low numbers. LOG2-B.HEX is a 16x zoom-in on the left end of LOG2-A.HEX. At that point, the worst
output error in LOG2-A.HEX is still under 0.02% from rounding and granularity; and below that point you can get more
resolution back by going to the LOG2-B.HEX table.
Remember that to get the log of numbers below 1, you just invert the argument, then negate the answer.
ALOG2-A.HEX, with offsets for programming into banks 4 and 5 ($4:0000-5:FFFF) of ROM 1, is just the reverse of LOG2-A.HEX
above. The input is the fractional part of the number to get the base-2 antilog of, leaving the integer part to the
user to handle separately, in order to yield more significant figures. So for inputs of 1 (scaled) and higher, strip
off the integer part and keep it aside, look up the antilog of the fractional part in the table, then shift it left by
however many bits the previously stripped-off integer part says (possibly requiring re-scaling). The range of the
unsigned input of the table is 0 to .9999847 scaled by 65,536. The unsigned output also has the same range and scale.
This can be considered the base-2-antilog version of the ex-1 function sometimes offered on calculators for better
resolution on low numbers. ALOG2-B.HEX is a 16x zoom-in on the left end of ALOG2-A.HEX. At that point, the worst
output error in ALOG2-A.HEX is still only about 0.03%; and below that point you can get more resolution back by going
to the ALOG2-B.HEX table.
Remember that to get the antilog of negative numbers, you just change the sign of the argument, then invert the answer.
LOG2-B.HEX, with offsets for programming into banks 6 and 7 ($6:0000-7:FFFF) of ROM 1, is a 128K table that is a zoom-in on
the left end of LOG2-A.HEX, expanded by a factor of 16, so the input has four more significant bits. The unsigned
input is limited to the range of 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576), while
the output range is 0 to .0874615 scaled by 2^19 (ie, 524,288), which comes out to $B31F (45,855 in decimal). So to
clarify: there are 65,536 two-byte cells; but keeping a binary scale factor on the output to keep it more compatible
with LOG2-A.HEX (because it is a zoom-in on its left end) means the output does not reach $FFFF.
Note that LOG2-A.HEX and LOG2-B.HEX are actually the base-2 log version of what is sometimes offered on calculators
as the ln(1+X) function for better resolution for logs of numbers very close to 1 (and very close to 0 in the ln(1+X)
function). If you go below approximately .0015 for input on the LOG2_B.HEX table, you will get the best answer by
simply saying that ln(1+X)≈X (similar to how the sine and the tangent of very small angles are basically the same).
It's not that there's anything wrong with the table, but that with the scaled input and output being only a few hundred
or less, the resolution is lost more and more as you go down. Remember however that the ln(1+X)≈X approximation for
low numbers is for the natural log, whereas the table is for the base-2 log; so convert accordingly!
ALOG2-B.HEX, with offsets for programming into banks 8 and 9 ($8:0000-9:FFFF) of ROM 1, is a 128K table that is basically the
reverse of LOG2-B.HEX, but in this case, a 16x zoom-in on the left end of ALOG2-A.HEX; so the range of its unsigned
input is from 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576). The output then ranges
from 0 to .0442731 also scaled by 2^20, which comes out to $B558 (46,424 in decimal). So to clarify: there are 65,536
two-byte cells; but keeping a binary scale factor on the output to keep it more compatible with ALOG2-A.HEX (because it
is a zoom-in on its left end) means that the output does not reach $FFFF.
Note that ALOG2-A.HEX and ALOG2-B.HEX are actually the base-2 antilog version of what is sometimes offered on
calculators as the ex-1 function for better resolution for antilogs of numbers very close to 0. If you go much below
approximately .001 for input on the ALOG2-B.HEX table, you will get the best answer by simply saying that ex-1≈X
(similar to how the sine and the tangent of very small angles are basically the same). It's not that there's anything
wrong with the table, but that with the scaled input and output being only a few hundred or less, the resolution is
lost more and more as you go down. Remember however that the ex-1≈X approximation for low numbers is for the natural
antilog, whereas the table is for the base-2 antilog; so convert accordingly!
For the ln(1+X) and ex-1 functions, use the LOG2-A.HEX, LOG2-B.HEX, ALOG2-A.HEX, and ALOG2-B.HEX tables, and the notes above
that go with them. Hyperbolic and inverse hyperbolic functions, and certain financial calculations, evaluate the expressions
ln(1+x) and ex-1 for arguments near zero and with results also near zero. The log & antilog tables with the -A and -B in
their file names allow greater accuracy in such calculations. There is a discussion of how to get ex-1 on a calculator
that's lacking that function, on the HP museum calculator forum, at http://hpmuseum.org/forum/thread-5508.html .
ln.HEX does not exist here. For ln (natural log): Since you'll normally have a scale factor anyway, just calculate the ln
(natural log) from the base-2 log. The conversion is:
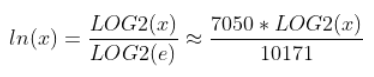 (You'd have to go out more than 8 digits to get to the error.)
The fact that you'll normally have a scale factor anyway means that including the scale factors above does not add any
multiplications or divisions to the run-time code. You just calculate the adjusted scale factors as constants before
assembling or compiling your program.
Another way to look at it is that the LOG2.HEX table is the natural-log table, with its output scaled by 5909.197
instead of 4096.
Aln.HEX does not exist here. For ln-1 (natural antilog): Since you'll normally have a scale factor anyway, just calculate
ln-1 from the base-2 antilog. The conversion is:
(You'd have to go out more than 8 digits to get to the error.)
The fact that you'll normally have a scale factor anyway means that including the scale factors above does not add any
multiplications or divisions to the run-time code. You just calculate the adjusted scale factors as constants before
assembling or compiling your program.
Another way to look at it is that the LOG2.HEX table is the natural-log table, with its output scaled by 5909.197
instead of 4096.
Aln.HEX does not exist here. For ln-1 (natural antilog): Since you'll normally have a scale factor anyway, just calculate
ln-1 from the base-2 antilog. The conversion is:
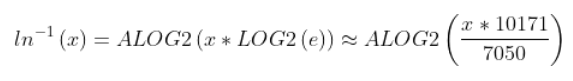 For further improved accuracy, you can use 36744/25469, which is LOG2(e) with an error of 9.8E-11 or .0000000098%.
10171/7050 above has an error of -3.8E-9 or .00000038%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the ALOG2.HEX table is the natural antilog table, with its input scaled by 5909.197
instead of 4096.
LOG10.HEX and ALOG10.HEX do not exist here. Since you'll normally have a scale factor anyway, LOG10 (common log) & ALOG10
(common antilog) can also be handled like ln & ln-1 above:
For further improved accuracy, you can use 36744/25469, which is LOG2(e) with an error of 9.8E-11 or .0000000098%.
10171/7050 above has an error of -3.8E-9 or .00000038%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the ALOG2.HEX table is the natural antilog table, with its input scaled by 5909.197
instead of 4096.
LOG10.HEX and ALOG10.HEX do not exist here. Since you'll normally have a scale factor anyway, LOG10 (common log) & ALOG10
(common antilog) can also be handled like ln & ln-1 above:
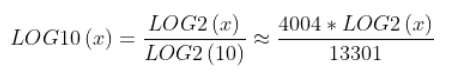 and:
and:
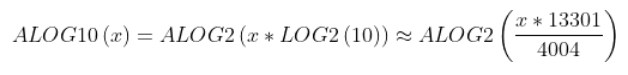 For further improved accuracy, you can use 42039/12655, which is LOG2(10) with an error of -9.7E-10, or -.000000097%.
The next pair I have is outside the 16-bit range: 70777/21306, which has an error of -1.5E-10, or -.000000015%.
13301/4004 above has an error of -6.9E-9, or -.00000069%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the LOG2.HEX table is the common-log table, with its output scaled by 13606.43
instead of 4096, and that ALOG2.HEX is the common antilog table, with its input scaled by that same number.
SQRT1.HEX is a 64K table of square roots. Input is 16-bit (unsigned), and output is 8-bit. For bank A ($A:0000-A:FFFF) of ROM
1. Output is truncated in this one, not rounded to the nearest integer. Even for getting the 16-bit root of a 32-bit
input, the table can serve to give the r=(x+r²)/2r method a better starting point so you don't need so many iterations.
SQRT2.HEX is another 64K table of square roots. Like SQRT1.HEX, input is 16-bit (unsigned) and output is 8-bit; but unlike
SQRT1.HEX, this one is rounded. Max output is of course $FF, not $100. For bank B ($B:0000-B:FFFF) of ROM 1.
SQRT3.HEX is a 128K table of square roots. Output is 16-bit. Input in a sense is 32-bit (unsigned); but with only 64K cells,
it assumes the 16 input bits are actually the high 16 bits of a 32-bit input whose low cell is 0000. Output is rounded.
For 32-bit input numbers whose low cell is not 0000, interpolating may bring a few more bits of accuracy.
For banks C & D ($C:0000-D:FFFF) of ROM 1.
BITREV.HEX is actually a set of bit-reversing tables, particularly useful for the fast Fourier transform. The 9-bit to 14-bit
tables take two bytes per cell, and the tables from 8-bit down to 2-bit take one byte per cell. The bits of interest
are right-justified, so for example a 5-bit field 00010011 becomes 00011001, with the five bits of interest remaining
on the right, and the unused 0's on the left remaining on the left. The set is supplied for bank F ($F:0000-F:FFFF) of
ROM 0 (not ROM 1), but since it is actually made up of many tables, here are the addresses of each table:
14-bit: $F:0000-F:7FFF ie, 32KB
13-bit: $F:8000-F:BFFF ie, 16KB
12-bit: $F:C000-F:DFFF ie, 8KB
11-bit: $F:E000-F:EFFF ie, 4KB
10-bit: $F:F000-F:F7FF ie, 2KB
9-bit: $F:F800-F:FBFF ie, 1KB
8-bit: $F:FC00-F:FCFF ie, 256 bytes
7-bit: $F:FE00-F:FE7F ie, 128 bytes
6-bit: $F:FF00-F:FF3F ie, 64 bytes
5-bit: $F:FF80-F:FF9F ie, 32 bytes
4-bit: $F:FFC0-F:FFCF ie, 16 bytes
3-bit: $F:FFE0-F:FFE7 ie, 8 bytes
2-bit: $F:FFF0-F:FFF3 ie, 4 bytes
As with the other hex files, the bytes of two-byte cells are reversed so they're low-byte-first. Note however that
there are gaps between the tables from 8-bit on down. That is because these tables have only one byte per cell; but
the starting addresses were chosen to make it easier to make them a function of the number of bits if you want to do
that.
BITREV15.HEX is the 15-bit bit-reversing table, with two bytes per cell. The offsets are provided for bank E (E:0000-E:FFFF),
but I am leaving it out of the EPROMs because the other files fill them and it is unlikely that anyone would be doing
32K-point FFTs on the low-end computers these files are intended for. The biggest FFT I've never done was 16K points,
and that was on the HP-71 computer, not a 65-family one.
MULT.HEX is the 128K multiplication table with offsets for programming into banks E and F ($E:0000-$F:FFFF) of ROM 1. Unsigned.
It's like the multiplication table you had in 3rd grade, but going from 0x0 up to 255x255 instead of only 12x12.
(Also see the way to multiply by using the table of squares above, under the SQUARE.HEX entry.)
Summary of which tables are in which EPROMs, as I supply them:
ROM0: banks: (I'm calling a 64KB section a "bank," as on the 65816 microprocessor)
SQUARE 0-3
INVERT 4-7
SIN 8-9
ASIN A-B
ATAN C
LOG2 D-E
BITREV F
ROM1:
ALOG2 0-1
LOG2-A 2-3
ALOG2-A 4-5
LOG2-B 6-7
ALOG2-B 8-9
SQRT1 A
SQRT2 B
SQRT3 C-D
MULT E-F
For further improved accuracy, you can use 42039/12655, which is LOG2(10) with an error of -9.7E-10, or -.000000097%.
The next pair I have is outside the 16-bit range: 70777/21306, which has an error of -1.5E-10, or -.000000015%.
13301/4004 above has an error of -6.9E-9, or -.00000069%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the LOG2.HEX table is the common-log table, with its output scaled by 13606.43
instead of 4096, and that ALOG2.HEX is the common antilog table, with its input scaled by that same number.
SQRT1.HEX is a 64K table of square roots. Input is 16-bit (unsigned), and output is 8-bit. For bank A ($A:0000-A:FFFF) of ROM
1. Output is truncated in this one, not rounded to the nearest integer. Even for getting the 16-bit root of a 32-bit
input, the table can serve to give the r=(x+r²)/2r method a better starting point so you don't need so many iterations.
SQRT2.HEX is another 64K table of square roots. Like SQRT1.HEX, input is 16-bit (unsigned) and output is 8-bit; but unlike
SQRT1.HEX, this one is rounded. Max output is of course $FF, not $100. For bank B ($B:0000-B:FFFF) of ROM 1.
SQRT3.HEX is a 128K table of square roots. Output is 16-bit. Input in a sense is 32-bit (unsigned); but with only 64K cells,
it assumes the 16 input bits are actually the high 16 bits of a 32-bit input whose low cell is 0000. Output is rounded.
For 32-bit input numbers whose low cell is not 0000, interpolating may bring a few more bits of accuracy.
For banks C & D ($C:0000-D:FFFF) of ROM 1.
BITREV.HEX is actually a set of bit-reversing tables, particularly useful for the fast Fourier transform. The 9-bit to 14-bit
tables take two bytes per cell, and the tables from 8-bit down to 2-bit take one byte per cell. The bits of interest
are right-justified, so for example a 5-bit field 00010011 becomes 00011001, with the five bits of interest remaining
on the right, and the unused 0's on the left remaining on the left. The set is supplied for bank F ($F:0000-F:FFFF) of
ROM 0 (not ROM 1), but since it is actually made up of many tables, here are the addresses of each table:
14-bit: $F:0000-F:7FFF ie, 32KB
13-bit: $F:8000-F:BFFF ie, 16KB
12-bit: $F:C000-F:DFFF ie, 8KB
11-bit: $F:E000-F:EFFF ie, 4KB
10-bit: $F:F000-F:F7FF ie, 2KB
9-bit: $F:F800-F:FBFF ie, 1KB
8-bit: $F:FC00-F:FCFF ie, 256 bytes
7-bit: $F:FE00-F:FE7F ie, 128 bytes
6-bit: $F:FF00-F:FF3F ie, 64 bytes
5-bit: $F:FF80-F:FF9F ie, 32 bytes
4-bit: $F:FFC0-F:FFCF ie, 16 bytes
3-bit: $F:FFE0-F:FFE7 ie, 8 bytes
2-bit: $F:FFF0-F:FFF3 ie, 4 bytes
As with the other hex files, the bytes of two-byte cells are reversed so they're low-byte-first. Note however that
there are gaps between the tables from 8-bit on down. That is because these tables have only one byte per cell; but
the starting addresses were chosen to make it easier to make them a function of the number of bits if you want to do
that.
BITREV15.HEX is the 15-bit bit-reversing table, with two bytes per cell. The offsets are provided for bank E (E:0000-E:FFFF),
but I am leaving it out of the EPROMs because the other files fill them and it is unlikely that anyone would be doing
32K-point FFTs on the low-end computers these files are intended for. The biggest FFT I've never done was 16K points,
and that was on the HP-71 computer, not a 65-family one.
MULT.HEX is the 128K multiplication table with offsets for programming into banks E and F ($E:0000-$F:FFFF) of ROM 1. Unsigned.
It's like the multiplication table you had in 3rd grade, but going from 0x0 up to 255x255 instead of only 12x12.
(Also see the way to multiply by using the table of squares above, under the SQUARE.HEX entry.)
Summary of which tables are in which EPROMs, as I supply them:
ROM0: banks: (I'm calling a 64KB section a "bank," as on the 65816 microprocessor)
SQUARE 0-3
INVERT 4-7
SIN 8-9
ASIN A-B
ATAN C
LOG2 D-E
BITREV F
ROM1:
ALOG2 0-1
LOG2-A 2-3
ALOG2-A 4-5
LOG2-B 6-7
ALOG2-B 8-9
SQRT1 A
SQRT2 B
SQRT3 C-D
MULT E-F
last updated May 5, 2020 contact: Garth Wilson, wilsonminesBdslextremeBcom
(replace the B's with @ and .)
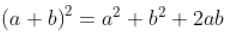 so if you solve for a*b, the multiplication becomes:
so if you solve for a*b, the multiplication becomes:
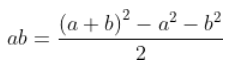 meaning it is reduced to an addition, three squarings (from the table), two subtractions, and a right shift.
There's also the MULT.HEX multiplication table at the end of ROM 1 (at the bottom here).
http://forum.6502.org/viewtopic.php?f=10&t=2211&p=20864#p20864 has an additional note about further simplifying a
multiplication for some situations.
INVERT.HEX is a 256K table of inverses. There are 65,536 cells of 4 bytes each, so input is 16-bit, and output is 32-bit.
Banks 4-7 ($4:0000-7:FFFF) of ROM 0. Looking up the 1st entry (1/0) should not be allowed, but result will show
FFFF:FFFF. Looking up the 2nd entry (1/1) should not be allowed, as the correct answer is 1:0000:0000, which cannot
be shown in 32 bits. Looking up 1/1 will show FFFF:FFFF also. This rounds to the nearest answer. Unsigned.
Inversion eases the otherwise slow division, because to divide, you can multiply by the inverse.
SIN.HEX is the 128K sin table with offsets for programming into banks 8 and 9 ($8:0000-$9:FFFF) of ROM 0. Positive outputs
are limited to $7FFF since $8000 is negative; so there are about 200 $7FFF's (at/near +90°) versus about 112 $8000's
(at/near -90°). The calling routine needs to trap inputs of $3FC7-$4039 unless the error is acceptable. See:
SIN ( $3FC6/2^16 * 360° ) = SIN ( 89.6814° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
SIN ( $3FC7/2^16 * 360° ) = SIN ( 89.6869° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $4039/2^16 * 360° ) = SIN ( 90.3131° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $403A/2^16 * 360° ) = SIN ( 90.3186° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
You can use SIN.HEX for cosines too by just adding $4000 (90°) to the input first.
ASIN.HEX is the 128K arcsin table with offsets for programming into banks A and B ($A:0000-B:FFFF) of ROM 0.
Outputs are limited to ±90° ($C000 to $4000) as on any calculator. Actually, the input range limitation prohibits
reaching +90° output, since +1, represented by $8000, becomes negative. The highest positive input then will be $7FFF,
whose output is $3FAF, or +89.555°. The routine using the table may need to trap that input to prevent an error.
It is important to note that this table is signed in the following way:
0 (represented by a $0000 input) to (nearly) 1 (maximum positive input being represented by $7FFF) outputs 0 (again
represented by $0000) to 89.555° (represented by ($3FAF). The next cell however, which is $8000 cells after the
beginning of the table, is negative, representing -1, and it outputs -90° (represented by $C000). As you advance
through the table from there, you approach 0° from the negative side, so the outputs move toward $FFFF before the
final cell which outputs $0000 as the granularity makes it round to 0°.
If you wanted to change the signing so that it starts at -1 and goes through 0 and goes to +1 without the discontinuity
in the middle, ie, that the table base would be the middle of the table and you go plus or minus from there, you could
edit-in the type-02 Intel Hex offset lines at the beginning of each of the two 64KB sections.
COS.HEX does not exist here. To get the cosine, just add 90° and take the sine.
ACOS.HEX does not exist here either. To get the arccosine, just take the arcsine and subtract the result from 90°.
TAN.HEX does not exist, because of tangent's nasty habit of going to infinity near 90°. To get practical resolution around 0°,
the scale factor would have to be such that the numbers get out of range long before 90°. So to get a tangent, take the
sine and the cosine of the angle, and then the program that needs the tangent can use the fraction as in Forth's */ ,
crank in a scale factor before dividing sine by cosine to get the tangent, or convert to a 32-bit tangent.
ATAN.HEX is the 64K-plus-one-cell table of arctangents for 0-45°, with offsets for programming into bank C ($C:0000-$D:0001)
of ROM 0. Since it takes one additional cell, and the table of base-2 logarithms has no use for a cell 0, that log2
table should follow. Unsigned.
The input is scaled by $8000, so 1.00000 is represented by $8000. 1.00000 is of course the tangent of 45°. The output
is again in the 16-bit circle, but its 45° maximum is represented by $2000. The first 45° are enough to get the rest of
the ±90° like you get with a calculator with a single input, or the whole circle if the calling routine takes in two
signed numbers as a fraction (y/x instead of x,y). (Since the table tops out at 45°, it could be scaled to give 1, 2,
or 3 more bits of precision, but I figured that would unnecessarily complicate things for most operations.)
Because of the problem mentioned above of the tangent easily going out of range near ±90°, it's better to use this
arctangent look-up table for 0-45° and get the rest of the circle from there. Here's how you do that. (I might post
code later.)
For single-number input: If the absolute value of the input is greater than 1.00000 (however you have it scaled),
invert it, look up the arctangent, and subtract that result from 90°. Apply the input sign to the output. As always,
scale factor and range must be heeded.
For dual-number (fractional) input n1/n2: The n1 & n2 are y and x, not vice-versa. Record the signs of the two input
numbers. If both are positive, you're in the 1st (top-right) quadrant (0-90°); if both negative, the 3rd (bottom-left,
180-270°); if n1 (the y value) is the only negative one, then you're in the 4th (bottom-right) quadrant (0 to -90°);
and if n2 (the x value) is the only negative one, then you're in the 2nd (top-left) quadrant (90-180°). Record that,
then take the absolute values of both numbers. If the numerator is greater than the denominator, swap them. Multiply
the numerator (whichever one that is now) by $8000 and divide the double-precision intermediate result by the
denominator, and look up the arctangent value from the table. If you had swapped numerator and denominator first,
subtract the result from 90°. Now you need to put it in the correct quadrant. For 1st quadrant (from above), leave it
alone. For 2nd quadrant, subtract the angle from 180°. For 3rd, add 180°. For 4th, subtract the angle from 360°.
LOG2.HEX is the 128K base-2 log table with offsets for programming into banks D and E ($D:0002-$E:FFFF) of ROM 0. Since you
can't take the log of 0, it has no use for address $D:0000; and since the arctangent table needs it, this log2 table
should immediately follow the arctan table. Input unscaled. Output scaled by 4096. Unsigned.
To get better precision in the base-2 log of smaller numbers, remember that scaling is as easy as shifting at the input
and subtracting at the output. The input is unscaled, going from 1 all the way to 65,535 (which also gives an output
of 65,535); but if the maximum input at some part of your program for example is only 200 and you want better resolution
in the low numbers as well as logs of numbers below 1 (ie, the output is negative), you can make (almost) 256 the
maximum input and scale it by 2^8 or 256 (or $100), then subtract 8*4096 (ie, 32768, or $8000) from the output. Then
the scaled input will have a range of .00390625 to 255.996, and the output range will be -8 (yes, now signed) to +7.9999
instead of 0 to 15.9998 (still scaled by 4096). You can go further, but remember to take care of the signs when the
output becomes so negative that it again becomes positive. Another way to get the negative logs is of course to invert
the input and then make the output negative, which may not even take any extra time if for example you got the input
number by diving two other numbers, and you could just swap the numerator and denominator and maybe use a different
scale factor if appropriate. For logs of numbers very close to 1, the LOG2-A.HEX and LOG2-B.HEX tables are better.
In the remote chance that you need bigger numbers, you can do the opposite, and shift the input to the right and add the
number of the shifts to the output (which will require re-scaling to stay within the 16-bit limitation). But read on...
The LOG2A.HEX file below allows (with more overhead) the forming of the log of any positive non-0 number, since the
integer part of the log is handled by the user's calling routine, and the table only does the fractional part.
BITREV.HEX goes here in bank F of ROM 0, but is described at the end, to keep the continuity in the log tables' descriptions.
ALOG2.HEX is the 128K base-2 antilog table with offsets for programming into banks 0 and 1 ($0:0000-1:FFFF) of ROM 1.
Input scaled by 4096. Output unscaled. Unsigned. For better resolution with smaller inputs and outputs, remember you
can do the reverse of what is discussed above in the LOG2 section above. For antilogs of numbers very close to 0, the
ALOG2-A.HEX and ALOG2-B.HEX tables will be better.
LOG2-A.HEX, with offsets for programming into banks 2 and 3 ($2:0000-3:FFFF) of ROM 1, is a 128K table similar to LOG2.HEX, but
this one leaves the integer part of the log to the user, in order to yield more significant figures. The unsigned
input is limited to the range of 0 to .999985 scaled by 65,536. You cannot take the log of 0 of course; but the 0 here
is the next digit after the first "1" digit found by the user's program as it shifts the input number left until that
first "1" bit is shifted out. You count the number of times you have to shift left for that to happen, and subtract
it from your constant that tells what range you're in, to get the integer part of the log answer. The fractional part
comes from the table, and is scaled the same way. Obviously it requires a little more thought to use this one than
ALOG2.HEX, but the reward is more precision. Answers are rounded to the nearest value that can be represented in the
table.
This can be considered the base-2-log version of the ln(1+X) function sometimes offered on calculators for better
resolution on low numbers. LOG2-B.HEX is a 16x zoom-in on the left end of LOG2-A.HEX. At that point, the worst
output error in LOG2-A.HEX is still under 0.02% from rounding and granularity; and below that point you can get more
resolution back by going to the LOG2-B.HEX table.
Remember that to get the log of numbers below 1, you just invert the argument, then negate the answer.
ALOG2-A.HEX, with offsets for programming into banks 4 and 5 ($4:0000-5:FFFF) of ROM 1, is just the reverse of LOG2-A.HEX
above. The input is the fractional part of the number to get the base-2 antilog of, leaving the integer part to the
user to handle separately, in order to yield more significant figures. So for inputs of 1 (scaled) and higher, strip
off the integer part and keep it aside, look up the antilog of the fractional part in the table, then shift it left by
however many bits the previously stripped-off integer part says (possibly requiring re-scaling). The range of the
unsigned input of the table is 0 to .9999847 scaled by 65,536. The unsigned output also has the same range and scale.
This can be considered the base-2-antilog version of the ex-1 function sometimes offered on calculators for better
resolution on low numbers. ALOG2-B.HEX is a 16x zoom-in on the left end of ALOG2-A.HEX. At that point, the worst
output error in ALOG2-A.HEX is still only about 0.03%; and below that point you can get more resolution back by going
to the ALOG2-B.HEX table.
Remember that to get the antilog of negative numbers, you just change the sign of the argument, then invert the answer.
LOG2-B.HEX, with offsets for programming into banks 6 and 7 ($6:0000-7:FFFF) of ROM 1, is a 128K table that is a zoom-in on
the left end of LOG2-A.HEX, expanded by a factor of 16, so the input has four more significant bits. The unsigned
input is limited to the range of 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576), while
the output range is 0 to .0874615 scaled by 2^19 (ie, 524,288), which comes out to $B31F (45,855 in decimal). So to
clarify: there are 65,536 two-byte cells; but keeping a binary scale factor on the output to keep it more compatible
with LOG2-A.HEX (because it is a zoom-in on its left end) means the output does not reach $FFFF.
Note that LOG2-A.HEX and LOG2-B.HEX are actually the base-2 log version of what is sometimes offered on calculators
as the ln(1+X) function for better resolution for logs of numbers very close to 1 (and very close to 0 in the ln(1+X)
function). If you go below approximately .0015 for input on the LOG2_B.HEX table, you will get the best answer by
simply saying that ln(1+X)≈X (similar to how the sine and the tangent of very small angles are basically the same).
It's not that there's anything wrong with the table, but that with the scaled input and output being only a few hundred
or less, the resolution is lost more and more as you go down. Remember however that the ln(1+X)≈X approximation for
low numbers is for the natural log, whereas the table is for the base-2 log; so convert accordingly!
ALOG2-B.HEX, with offsets for programming into banks 8 and 9 ($8:0000-9:FFFF) of ROM 1, is a 128K table that is basically the
reverse of LOG2-B.HEX, but in this case, a 16x zoom-in on the left end of ALOG2-A.HEX; so the range of its unsigned
input is from 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576). The output then ranges
from 0 to .0442731 also scaled by 2^20, which comes out to $B558 (46,424 in decimal). So to clarify: there are 65,536
two-byte cells; but keeping a binary scale factor on the output to keep it more compatible with ALOG2-A.HEX (because it
is a zoom-in on its left end) means that the output does not reach $FFFF.
Note that ALOG2-A.HEX and ALOG2-B.HEX are actually the base-2 antilog version of what is sometimes offered on
calculators as the ex-1 function for better resolution for antilogs of numbers very close to 0. If you go much below
approximately .001 for input on the ALOG2-B.HEX table, you will get the best answer by simply saying that ex-1≈X
(similar to how the sine and the tangent of very small angles are basically the same). It's not that there's anything
wrong with the table, but that with the scaled input and output being only a few hundred or less, the resolution is
lost more and more as you go down. Remember however that the ex-1≈X approximation for low numbers is for the natural
antilog, whereas the table is for the base-2 antilog; so convert accordingly!
For the ln(1+X) and ex-1 functions, use the LOG2-A.HEX, LOG2-B.HEX, ALOG2-A.HEX, and ALOG2-B.HEX tables, and the notes above
that go with them. Hyperbolic and inverse hyperbolic functions, and certain financial calculations, evaluate the expressions
ln(1+x) and ex-1 for arguments near zero and with results also near zero. The log & antilog tables with the -A and -B in
their file names allow greater accuracy in such calculations. There is a discussion of how to get ex-1 on a calculator
that's lacking that function, on the HP museum calculator forum, at http://hpmuseum.org/forum/thread-5508.html .
ln.HEX does not exist here. For ln (natural log): Since you'll normally have a scale factor anyway, just calculate the ln
(natural log) from the base-2 log. The conversion is:
meaning it is reduced to an addition, three squarings (from the table), two subtractions, and a right shift.
There's also the MULT.HEX multiplication table at the end of ROM 1 (at the bottom here).
http://forum.6502.org/viewtopic.php?f=10&t=2211&p=20864#p20864 has an additional note about further simplifying a
multiplication for some situations.
INVERT.HEX is a 256K table of inverses. There are 65,536 cells of 4 bytes each, so input is 16-bit, and output is 32-bit.
Banks 4-7 ($4:0000-7:FFFF) of ROM 0. Looking up the 1st entry (1/0) should not be allowed, but result will show
FFFF:FFFF. Looking up the 2nd entry (1/1) should not be allowed, as the correct answer is 1:0000:0000, which cannot
be shown in 32 bits. Looking up 1/1 will show FFFF:FFFF also. This rounds to the nearest answer. Unsigned.
Inversion eases the otherwise slow division, because to divide, you can multiply by the inverse.
SIN.HEX is the 128K sin table with offsets for programming into banks 8 and 9 ($8:0000-$9:FFFF) of ROM 0. Positive outputs
are limited to $7FFF since $8000 is negative; so there are about 200 $7FFF's (at/near +90°) versus about 112 $8000's
(at/near -90°). The calling routine needs to trap inputs of $3FC7-$4039 unless the error is acceptable. See:
SIN ( $3FC6/2^16 * 360° ) = SIN ( 89.6814° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
SIN ( $3FC7/2^16 * 360° ) = SIN ( 89.6869° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $4039/2^16 * 360° ) = SIN ( 90.3131° ) = .9999851 = 32,767.51/32,768 -- Trap input for accuracy at 90°.
SIN ( $403A/2^16 * 360° ) = SIN ( 90.3186° ) = .9999845 = 32,767.49/32,768 -- Normal. Rounds output to $7FFF.
You can use SIN.HEX for cosines too by just adding $4000 (90°) to the input first.
ASIN.HEX is the 128K arcsin table with offsets for programming into banks A and B ($A:0000-B:FFFF) of ROM 0.
Outputs are limited to ±90° ($C000 to $4000) as on any calculator. Actually, the input range limitation prohibits
reaching +90° output, since +1, represented by $8000, becomes negative. The highest positive input then will be $7FFF,
whose output is $3FAF, or +89.555°. The routine using the table may need to trap that input to prevent an error.
It is important to note that this table is signed in the following way:
0 (represented by a $0000 input) to (nearly) 1 (maximum positive input being represented by $7FFF) outputs 0 (again
represented by $0000) to 89.555° (represented by ($3FAF). The next cell however, which is $8000 cells after the
beginning of the table, is negative, representing -1, and it outputs -90° (represented by $C000). As you advance
through the table from there, you approach 0° from the negative side, so the outputs move toward $FFFF before the
final cell which outputs $0000 as the granularity makes it round to 0°.
If you wanted to change the signing so that it starts at -1 and goes through 0 and goes to +1 without the discontinuity
in the middle, ie, that the table base would be the middle of the table and you go plus or minus from there, you could
edit-in the type-02 Intel Hex offset lines at the beginning of each of the two 64KB sections.
COS.HEX does not exist here. To get the cosine, just add 90° and take the sine.
ACOS.HEX does not exist here either. To get the arccosine, just take the arcsine and subtract the result from 90°.
TAN.HEX does not exist, because of tangent's nasty habit of going to infinity near 90°. To get practical resolution around 0°,
the scale factor would have to be such that the numbers get out of range long before 90°. So to get a tangent, take the
sine and the cosine of the angle, and then the program that needs the tangent can use the fraction as in Forth's */ ,
crank in a scale factor before dividing sine by cosine to get the tangent, or convert to a 32-bit tangent.
ATAN.HEX is the 64K-plus-one-cell table of arctangents for 0-45°, with offsets for programming into bank C ($C:0000-$D:0001)
of ROM 0. Since it takes one additional cell, and the table of base-2 logarithms has no use for a cell 0, that log2
table should follow. Unsigned.
The input is scaled by $8000, so 1.00000 is represented by $8000. 1.00000 is of course the tangent of 45°. The output
is again in the 16-bit circle, but its 45° maximum is represented by $2000. The first 45° are enough to get the rest of
the ±90° like you get with a calculator with a single input, or the whole circle if the calling routine takes in two
signed numbers as a fraction (y/x instead of x,y). (Since the table tops out at 45°, it could be scaled to give 1, 2,
or 3 more bits of precision, but I figured that would unnecessarily complicate things for most operations.)
Because of the problem mentioned above of the tangent easily going out of range near ±90°, it's better to use this
arctangent look-up table for 0-45° and get the rest of the circle from there. Here's how you do that. (I might post
code later.)
For single-number input: If the absolute value of the input is greater than 1.00000 (however you have it scaled),
invert it, look up the arctangent, and subtract that result from 90°. Apply the input sign to the output. As always,
scale factor and range must be heeded.
For dual-number (fractional) input n1/n2: The n1 & n2 are y and x, not vice-versa. Record the signs of the two input
numbers. If both are positive, you're in the 1st (top-right) quadrant (0-90°); if both negative, the 3rd (bottom-left,
180-270°); if n1 (the y value) is the only negative one, then you're in the 4th (bottom-right) quadrant (0 to -90°);
and if n2 (the x value) is the only negative one, then you're in the 2nd (top-left) quadrant (90-180°). Record that,
then take the absolute values of both numbers. If the numerator is greater than the denominator, swap them. Multiply
the numerator (whichever one that is now) by $8000 and divide the double-precision intermediate result by the
denominator, and look up the arctangent value from the table. If you had swapped numerator and denominator first,
subtract the result from 90°. Now you need to put it in the correct quadrant. For 1st quadrant (from above), leave it
alone. For 2nd quadrant, subtract the angle from 180°. For 3rd, add 180°. For 4th, subtract the angle from 360°.
LOG2.HEX is the 128K base-2 log table with offsets for programming into banks D and E ($D:0002-$E:FFFF) of ROM 0. Since you
can't take the log of 0, it has no use for address $D:0000; and since the arctangent table needs it, this log2 table
should immediately follow the arctan table. Input unscaled. Output scaled by 4096. Unsigned.
To get better precision in the base-2 log of smaller numbers, remember that scaling is as easy as shifting at the input
and subtracting at the output. The input is unscaled, going from 1 all the way to 65,535 (which also gives an output
of 65,535); but if the maximum input at some part of your program for example is only 200 and you want better resolution
in the low numbers as well as logs of numbers below 1 (ie, the output is negative), you can make (almost) 256 the
maximum input and scale it by 2^8 or 256 (or $100), then subtract 8*4096 (ie, 32768, or $8000) from the output. Then
the scaled input will have a range of .00390625 to 255.996, and the output range will be -8 (yes, now signed) to +7.9999
instead of 0 to 15.9998 (still scaled by 4096). You can go further, but remember to take care of the signs when the
output becomes so negative that it again becomes positive. Another way to get the negative logs is of course to invert
the input and then make the output negative, which may not even take any extra time if for example you got the input
number by diving two other numbers, and you could just swap the numerator and denominator and maybe use a different
scale factor if appropriate. For logs of numbers very close to 1, the LOG2-A.HEX and LOG2-B.HEX tables are better.
In the remote chance that you need bigger numbers, you can do the opposite, and shift the input to the right and add the
number of the shifts to the output (which will require re-scaling to stay within the 16-bit limitation). But read on...
The LOG2A.HEX file below allows (with more overhead) the forming of the log of any positive non-0 number, since the
integer part of the log is handled by the user's calling routine, and the table only does the fractional part.
BITREV.HEX goes here in bank F of ROM 0, but is described at the end, to keep the continuity in the log tables' descriptions.
ALOG2.HEX is the 128K base-2 antilog table with offsets for programming into banks 0 and 1 ($0:0000-1:FFFF) of ROM 1.
Input scaled by 4096. Output unscaled. Unsigned. For better resolution with smaller inputs and outputs, remember you
can do the reverse of what is discussed above in the LOG2 section above. For antilogs of numbers very close to 0, the
ALOG2-A.HEX and ALOG2-B.HEX tables will be better.
LOG2-A.HEX, with offsets for programming into banks 2 and 3 ($2:0000-3:FFFF) of ROM 1, is a 128K table similar to LOG2.HEX, but
this one leaves the integer part of the log to the user, in order to yield more significant figures. The unsigned
input is limited to the range of 0 to .999985 scaled by 65,536. You cannot take the log of 0 of course; but the 0 here
is the next digit after the first "1" digit found by the user's program as it shifts the input number left until that
first "1" bit is shifted out. You count the number of times you have to shift left for that to happen, and subtract
it from your constant that tells what range you're in, to get the integer part of the log answer. The fractional part
comes from the table, and is scaled the same way. Obviously it requires a little more thought to use this one than
ALOG2.HEX, but the reward is more precision. Answers are rounded to the nearest value that can be represented in the
table.
This can be considered the base-2-log version of the ln(1+X) function sometimes offered on calculators for better
resolution on low numbers. LOG2-B.HEX is a 16x zoom-in on the left end of LOG2-A.HEX. At that point, the worst
output error in LOG2-A.HEX is still under 0.02% from rounding and granularity; and below that point you can get more
resolution back by going to the LOG2-B.HEX table.
Remember that to get the log of numbers below 1, you just invert the argument, then negate the answer.
ALOG2-A.HEX, with offsets for programming into banks 4 and 5 ($4:0000-5:FFFF) of ROM 1, is just the reverse of LOG2-A.HEX
above. The input is the fractional part of the number to get the base-2 antilog of, leaving the integer part to the
user to handle separately, in order to yield more significant figures. So for inputs of 1 (scaled) and higher, strip
off the integer part and keep it aside, look up the antilog of the fractional part in the table, then shift it left by
however many bits the previously stripped-off integer part says (possibly requiring re-scaling). The range of the
unsigned input of the table is 0 to .9999847 scaled by 65,536. The unsigned output also has the same range and scale.
This can be considered the base-2-antilog version of the ex-1 function sometimes offered on calculators for better
resolution on low numbers. ALOG2-B.HEX is a 16x zoom-in on the left end of ALOG2-A.HEX. At that point, the worst
output error in ALOG2-A.HEX is still only about 0.03%; and below that point you can get more resolution back by going
to the ALOG2-B.HEX table.
Remember that to get the antilog of negative numbers, you just change the sign of the argument, then invert the answer.
LOG2-B.HEX, with offsets for programming into banks 6 and 7 ($6:0000-7:FFFF) of ROM 1, is a 128K table that is a zoom-in on
the left end of LOG2-A.HEX, expanded by a factor of 16, so the input has four more significant bits. The unsigned
input is limited to the range of 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576), while
the output range is 0 to .0874615 scaled by 2^19 (ie, 524,288), which comes out to $B31F (45,855 in decimal). So to
clarify: there are 65,536 two-byte cells; but keeping a binary scale factor on the output to keep it more compatible
with LOG2-A.HEX (because it is a zoom-in on its left end) means the output does not reach $FFFF.
Note that LOG2-A.HEX and LOG2-B.HEX are actually the base-2 log version of what is sometimes offered on calculators
as the ln(1+X) function for better resolution for logs of numbers very close to 1 (and very close to 0 in the ln(1+X)
function). If you go below approximately .0015 for input on the LOG2_B.HEX table, you will get the best answer by
simply saying that ln(1+X)≈X (similar to how the sine and the tangent of very small angles are basically the same).
It's not that there's anything wrong with the table, but that with the scaled input and output being only a few hundred
or less, the resolution is lost more and more as you go down. Remember however that the ln(1+X)≈X approximation for
low numbers is for the natural log, whereas the table is for the base-2 log; so convert accordingly!
ALOG2-B.HEX, with offsets for programming into banks 8 and 9 ($8:0000-9:FFFF) of ROM 1, is a 128K table that is basically the
reverse of LOG2-B.HEX, but in this case, a 16x zoom-in on the left end of ALOG2-A.HEX; so the range of its unsigned
input is from 0 to (almost) 1/16th, actually to .06249905, scaled by 2^20 (ie, 1,048,576). The output then ranges
from 0 to .0442731 also scaled by 2^20, which comes out to $B558 (46,424 in decimal). So to clarify: there are 65,536
two-byte cells; but keeping a binary scale factor on the output to keep it more compatible with ALOG2-A.HEX (because it
is a zoom-in on its left end) means that the output does not reach $FFFF.
Note that ALOG2-A.HEX and ALOG2-B.HEX are actually the base-2 antilog version of what is sometimes offered on
calculators as the ex-1 function for better resolution for antilogs of numbers very close to 0. If you go much below
approximately .001 for input on the ALOG2-B.HEX table, you will get the best answer by simply saying that ex-1≈X
(similar to how the sine and the tangent of very small angles are basically the same). It's not that there's anything
wrong with the table, but that with the scaled input and output being only a few hundred or less, the resolution is
lost more and more as you go down. Remember however that the ex-1≈X approximation for low numbers is for the natural
antilog, whereas the table is for the base-2 antilog; so convert accordingly!
For the ln(1+X) and ex-1 functions, use the LOG2-A.HEX, LOG2-B.HEX, ALOG2-A.HEX, and ALOG2-B.HEX tables, and the notes above
that go with them. Hyperbolic and inverse hyperbolic functions, and certain financial calculations, evaluate the expressions
ln(1+x) and ex-1 for arguments near zero and with results also near zero. The log & antilog tables with the -A and -B in
their file names allow greater accuracy in such calculations. There is a discussion of how to get ex-1 on a calculator
that's lacking that function, on the HP museum calculator forum, at http://hpmuseum.org/forum/thread-5508.html .
ln.HEX does not exist here. For ln (natural log): Since you'll normally have a scale factor anyway, just calculate the ln
(natural log) from the base-2 log. The conversion is:
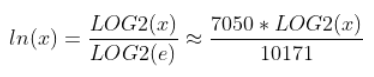 (You'd have to go out more than 8 digits to get to the error.)
The fact that you'll normally have a scale factor anyway means that including the scale factors above does not add any
multiplications or divisions to the run-time code. You just calculate the adjusted scale factors as constants before
assembling or compiling your program.
Another way to look at it is that the LOG2.HEX table is the natural-log table, with its output scaled by 5909.197
instead of 4096.
Aln.HEX does not exist here. For ln-1 (natural antilog): Since you'll normally have a scale factor anyway, just calculate
ln-1 from the base-2 antilog. The conversion is:
(You'd have to go out more than 8 digits to get to the error.)
The fact that you'll normally have a scale factor anyway means that including the scale factors above does not add any
multiplications or divisions to the run-time code. You just calculate the adjusted scale factors as constants before
assembling or compiling your program.
Another way to look at it is that the LOG2.HEX table is the natural-log table, with its output scaled by 5909.197
instead of 4096.
Aln.HEX does not exist here. For ln-1 (natural antilog): Since you'll normally have a scale factor anyway, just calculate
ln-1 from the base-2 antilog. The conversion is:
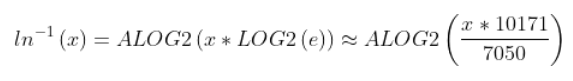 For further improved accuracy, you can use 36744/25469, which is LOG2(e) with an error of 9.8E-11 or .0000000098%.
10171/7050 above has an error of -3.8E-9 or .00000038%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the ALOG2.HEX table is the natural antilog table, with its input scaled by 5909.197
instead of 4096.
LOG10.HEX and ALOG10.HEX do not exist here. Since you'll normally have a scale factor anyway, LOG10 (common log) & ALOG10
(common antilog) can also be handled like ln & ln-1 above:
For further improved accuracy, you can use 36744/25469, which is LOG2(e) with an error of 9.8E-11 or .0000000098%.
10171/7050 above has an error of -3.8E-9 or .00000038%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the ALOG2.HEX table is the natural antilog table, with its input scaled by 5909.197
instead of 4096.
LOG10.HEX and ALOG10.HEX do not exist here. Since you'll normally have a scale factor anyway, LOG10 (common log) & ALOG10
(common antilog) can also be handled like ln & ln-1 above:
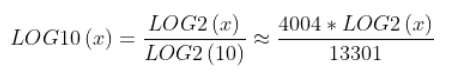 and:
and:
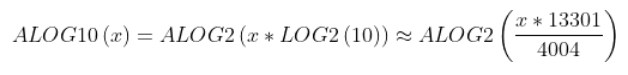 For further improved accuracy, you can use 42039/12655, which is LOG2(10) with an error of -9.7E-10, or -.000000097%.
The next pair I have is outside the 16-bit range: 70777/21306, which has an error of -1.5E-10, or -.000000015%.
13301/4004 above has an error of -6.9E-9, or -.00000069%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the LOG2.HEX table is the common-log table, with its output scaled by 13606.43
instead of 4096, and that ALOG2.HEX is the common antilog table, with its input scaled by that same number.
SQRT1.HEX is a 64K table of square roots. Input is 16-bit (unsigned), and output is 8-bit. For bank A ($A:0000-A:FFFF) of ROM
1. Output is truncated in this one, not rounded to the nearest integer. Even for getting the 16-bit root of a 32-bit
input, the table can serve to give the r=(x+r²)/2r method a better starting point so you don't need so many iterations.
SQRT2.HEX is another 64K table of square roots. Like SQRT1.HEX, input is 16-bit (unsigned) and output is 8-bit; but unlike
SQRT1.HEX, this one is rounded. Max output is of course $FF, not $100. For bank B ($B:0000-B:FFFF) of ROM 1.
SQRT3.HEX is a 128K table of square roots. Output is 16-bit. Input in a sense is 32-bit (unsigned); but with only 64K cells,
it assumes the 16 input bits are actually the high 16 bits of a 32-bit input whose low cell is 0000. Output is rounded.
For 32-bit input numbers whose low cell is not 0000, interpolating may bring a few more bits of accuracy.
For banks C & D ($C:0000-D:FFFF) of ROM 1.
BITREV.HEX is actually a set of bit-reversing tables, particularly useful for the fast Fourier transform. The 9-bit to 14-bit
tables take two bytes per cell, and the tables from 8-bit down to 2-bit take one byte per cell. The bits of interest
are right-justified, so for example a 5-bit field 00010011 becomes 00011001, with the five bits of interest remaining
on the right, and the unused 0's on the left remaining on the left. The set is supplied for bank F ($F:0000-F:FFFF) of
ROM 0 (not ROM 1), but since it is actually made up of many tables, here are the addresses of each table:
14-bit: $F:0000-F:7FFF ie, 32KB
13-bit: $F:8000-F:BFFF ie, 16KB
12-bit: $F:C000-F:DFFF ie, 8KB
11-bit: $F:E000-F:EFFF ie, 4KB
10-bit: $F:F000-F:F7FF ie, 2KB
9-bit: $F:F800-F:FBFF ie, 1KB
8-bit: $F:FC00-F:FCFF ie, 256 bytes
7-bit: $F:FE00-F:FE7F ie, 128 bytes
6-bit: $F:FF00-F:FF3F ie, 64 bytes
5-bit: $F:FF80-F:FF9F ie, 32 bytes
4-bit: $F:FFC0-F:FFCF ie, 16 bytes
3-bit: $F:FFE0-F:FFE7 ie, 8 bytes
2-bit: $F:FFF0-F:FFF3 ie, 4 bytes
As with the other hex files, the bytes of two-byte cells are reversed so they're low-byte-first. Note however that
there are gaps between the tables from 8-bit on down. That is because these tables have only one byte per cell; but
the starting addresses were chosen to make it easier to make them a function of the number of bits if you want to do
that.
BITREV15.HEX is the 15-bit bit-reversing table, with two bytes per cell. The offsets are provided for bank E (E:0000-E:FFFF),
but I am leaving it out of the EPROMs because the other files fill them and it is unlikely that anyone would be doing
32K-point FFTs on the low-end computers these files are intended for. The biggest FFT I've never done was 16K points,
and that was on the HP-71 computer, not a 65-family one.
MULT.HEX is the 128K multiplication table with offsets for programming into banks E and F ($E:0000-$F:FFFF) of ROM 1. Unsigned.
It's like the multiplication table you had in 3rd grade, but going from 0x0 up to 255x255 instead of only 12x12.
(Also see the way to multiply by using the table of squares above, under the SQUARE.HEX entry.)
Summary of which tables are in which EPROMs, as I supply them:
ROM0: banks: (I'm calling a 64KB section a "bank," as on the 65816 microprocessor)
SQUARE 0-3
INVERT 4-7
SIN 8-9
ASIN A-B
ATAN C
LOG2 D-E
BITREV F
ROM1:
ALOG2 0-1
LOG2-A 2-3
ALOG2-A 4-5
LOG2-B 6-7
ALOG2-B 8-9
SQRT1 A
SQRT2 B
SQRT3 C-D
MULT E-F
For further improved accuracy, you can use 42039/12655, which is LOG2(10) with an error of -9.7E-10, or -.000000097%.
The next pair I have is outside the 16-bit range: 70777/21306, which has an error of -1.5E-10, or -.000000015%.
13301/4004 above has an error of -6.9E-9, or -.00000069%, but the numbers fit within 16-bit signed cells.
Another way to look at it is that the LOG2.HEX table is the common-log table, with its output scaled by 13606.43
instead of 4096, and that ALOG2.HEX is the common antilog table, with its input scaled by that same number.
SQRT1.HEX is a 64K table of square roots. Input is 16-bit (unsigned), and output is 8-bit. For bank A ($A:0000-A:FFFF) of ROM
1. Output is truncated in this one, not rounded to the nearest integer. Even for getting the 16-bit root of a 32-bit
input, the table can serve to give the r=(x+r²)/2r method a better starting point so you don't need so many iterations.
SQRT2.HEX is another 64K table of square roots. Like SQRT1.HEX, input is 16-bit (unsigned) and output is 8-bit; but unlike
SQRT1.HEX, this one is rounded. Max output is of course $FF, not $100. For bank B ($B:0000-B:FFFF) of ROM 1.
SQRT3.HEX is a 128K table of square roots. Output is 16-bit. Input in a sense is 32-bit (unsigned); but with only 64K cells,
it assumes the 16 input bits are actually the high 16 bits of a 32-bit input whose low cell is 0000. Output is rounded.
For 32-bit input numbers whose low cell is not 0000, interpolating may bring a few more bits of accuracy.
For banks C & D ($C:0000-D:FFFF) of ROM 1.
BITREV.HEX is actually a set of bit-reversing tables, particularly useful for the fast Fourier transform. The 9-bit to 14-bit
tables take two bytes per cell, and the tables from 8-bit down to 2-bit take one byte per cell. The bits of interest
are right-justified, so for example a 5-bit field 00010011 becomes 00011001, with the five bits of interest remaining
on the right, and the unused 0's on the left remaining on the left. The set is supplied for bank F ($F:0000-F:FFFF) of
ROM 0 (not ROM 1), but since it is actually made up of many tables, here are the addresses of each table:
14-bit: $F:0000-F:7FFF ie, 32KB
13-bit: $F:8000-F:BFFF ie, 16KB
12-bit: $F:C000-F:DFFF ie, 8KB
11-bit: $F:E000-F:EFFF ie, 4KB
10-bit: $F:F000-F:F7FF ie, 2KB
9-bit: $F:F800-F:FBFF ie, 1KB
8-bit: $F:FC00-F:FCFF ie, 256 bytes
7-bit: $F:FE00-F:FE7F ie, 128 bytes
6-bit: $F:FF00-F:FF3F ie, 64 bytes
5-bit: $F:FF80-F:FF9F ie, 32 bytes
4-bit: $F:FFC0-F:FFCF ie, 16 bytes
3-bit: $F:FFE0-F:FFE7 ie, 8 bytes
2-bit: $F:FFF0-F:FFF3 ie, 4 bytes
As with the other hex files, the bytes of two-byte cells are reversed so they're low-byte-first. Note however that
there are gaps between the tables from 8-bit on down. That is because these tables have only one byte per cell; but
the starting addresses were chosen to make it easier to make them a function of the number of bits if you want to do
that.
BITREV15.HEX is the 15-bit bit-reversing table, with two bytes per cell. The offsets are provided for bank E (E:0000-E:FFFF),
but I am leaving it out of the EPROMs because the other files fill them and it is unlikely that anyone would be doing
32K-point FFTs on the low-end computers these files are intended for. The biggest FFT I've never done was 16K points,
and that was on the HP-71 computer, not a 65-family one.
MULT.HEX is the 128K multiplication table with offsets for programming into banks E and F ($E:0000-$F:FFFF) of ROM 1. Unsigned.
It's like the multiplication table you had in 3rd grade, but going from 0x0 up to 255x255 instead of only 12x12.
(Also see the way to multiply by using the table of squares above, under the SQUARE.HEX entry.)
Summary of which tables are in which EPROMs, as I supply them:
ROM0: banks: (I'm calling a 64KB section a "bank," as on the 65816 microprocessor)
SQUARE 0-3
INVERT 4-7
SIN 8-9
ASIN A-B
ATAN C
LOG2 D-E
BITREV F
ROM1:
ALOG2 0-1
LOG2-A 2-3
ALOG2-A 4-5
LOG2-B 6-7
ALOG2-B 8-9
SQRT1 A
SQRT2 B
SQRT3 C-D
MULT E-F